Derived Category Language 3
Derived Category Language 3
Language stability and triangulated category
[Epitome]
T. Bridgeland defined stability conditions on triangulated categories in 2007.
Language's stability presented by Sergej Karcevskij in 1928.
Bridgeland's stability seems to hint for Karcevskij's stability.
Stability conditions on triangulated categoriesData ( Z, A ) satisfies the next condition.
is bounded kernel of t-structure.
gives stability condition on A .
------------------------------------------------------------------------------------------------------
2.
[Paper on Karcevskij conjecture by TANAKA Akio 2011]
Condition of Meaning
TANAKA Akio
September 11, 2011
[Preparation]
Graded differential algebra 
Minimal model of graded differential algebra 
Degree of homogenious element x of graded differential algabra |x|
Basis of linear space is given by homogenious and elements x1, ....., xn
N (V) = L (V) k = N ( x 1 , ....., x n )
Operation of minimal model 
Spherical surface Sn, n≥2
de Rham complex 
*(Sn)
When n iseaven number,
Volume element of Sn 
Mn = Λ (x), |x| = n, dx = 0,
, 
M2n-1 gives minimal model Sn to de Rham complex 
.
When n is odd number,
Mn gives minimal model Sn to de Rham complex .
[Interpretation]
Word is given by spherical surface.
Meaning of word is given by elements x1, ....., xn.
Word has minimal model.
Word becomes formal.
Fundamental group of word contains free group of rank b1(M).
Here KARCEVSKIJ's "stable part" is identified to fundamental group and " mobile part" is identified to free group.
Refer to the paper Notes for KARVESKIJ Sergej "asymmetric Dusualisme the linguistic sign" .
--------------------------------------------------------------------------------------------
3.
[Paper on description of language by TANAKA Akio 2011]
Description of Language
TANAKA Akio
September 9, 2011
Manifold M
Cup product map of M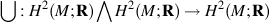 
Dual map of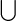 
Free Lie algebra that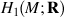 
generates £ ( 
)
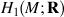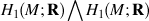is identified as the partial space of £( 
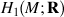) that quadrastic Lie bracket of 
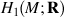generates.
Ideal of £(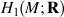 
) that Im η generates a
Holonomy Lie algebra of M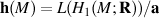 
Completion of holonomy Lie algebra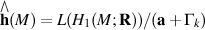 
If M has quadrastic homology connection, Malcev completion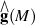 
becomes isomorphic with holonoly Lie algebra completion 
.
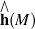Primary minimum model M(1)of differential manifold M is isomorphic with Malcev completion of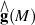 
of M's fundamental group.
For the description of a language model there is a need primary minimum model M(1) of differential manifold M.
This paper has been published by Sekinan Research Field of Language.
All rights reserved.
© 2011 by The Sekinan Research Field of Language
-----------------------------------------------------------------------------------------------------------
4.
[Note]
If word satisfies Bridgeland 2002's Data{Z, A] , word has a stability in language.
For the problem of additional meaning refer to Karcevskij conjecture 1928 and Kawamata conjecture 2002.
-----------------------------------------------------------------------------------------------------
#This paper is unfinished
Tokyo
25 May 2016
SRFL Theory